Abstract
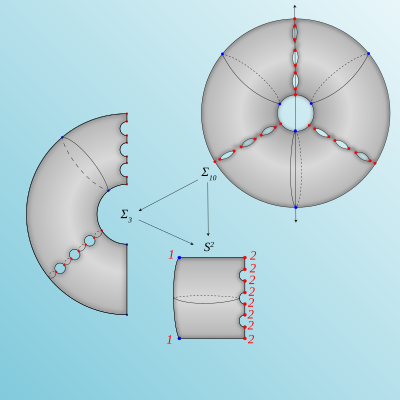
I will prove that every geometrically simply-connected four-manifold arises as a 3-fold irregular cover of $S^4$ branched along an embedded surface. This is a four-dimensional analogue of a classical result of Hilden and relies on adapting his technique to the context of trisections of four-manifolds and embedded surfaces. I’ll review the necessary tools and sketch out the proof.
Joint work with Blair, Cahn, Meier.