Abstract
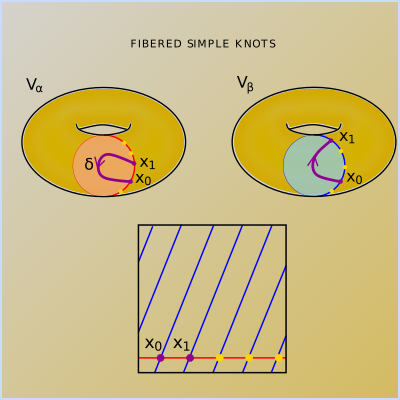
A simple knot is a knot in a lens space built from the union of a pair of properly embedded arcs, one in each of a pair of standard meridianal disks. We prove that a simple knot in the lens space $L(p, q)$ fibers if and only if its order in homology does not divide any remainder occurring in the Euclidean algorithm applied to the pair $(p,q)$. One corollary is that if $p = m^2$ is a perfect square, then any simple knot of order m fibers, answering a question of Cebanu. More generally, we compute in a similar way the leading coefficient of the Alexander polynomial of a simple knot. This is joint work with Josh Greene.